Deep Learning for Astronomical Image Processing

InTheArt Seminar, Nov. 20th 2020

François Lanusse










slides at eiffl.github.io/talks/ITA2020

the Rubin Observatory Legacy Survey of Space and Time

  • 1000 images each night, 15 TB/night for 10 years

  • 18,000 square degrees, observed once every few days

  • Tens of billions of objects, each one observed $\sim1000$ times

Previous generation survey: SDSS




















Image credit: Peter Melchior

Current generation survey: DES




















Image credit: Peter Melchior

LSST precursor survey: HSC




















Image credit: Peter Melchior

Outline of this talk



Where can Deep Learning help address the challenges of modern surveys ?



  • Low level image processing


  • Solving Inverse Problems


  • Probabilistic inference




Deep detection of gravitational lenses

Work in collaboration with:

Quanbin Ma, Nan Li, Thomas E. Collett, Chun-Liang Li, Siamak Ravanbakhsh, Rachel Mandelbaum, Barnabas Poczos




$\Longrightarrow$ Use Deep Neural Networks to detect rare objects
Huang et al. (2019) - arXiv:1906.00970

Galaxy-Galaxy Strong Lensing






example of application: gravitational time delays

WWAD: What Would an Astrophysicist Do ?

gri composite
g - $\alpha$ i
detected areas
HST images
RingFinder (Gavazzi et al. 2014)

Gavazzi et al. (2014), Collett (2015)

$\Longrightarrow$ Plainly intractable at the scale of LSST

A conventional Convolutional Neural Network


Preactivated Residual Unit
(He et al. 2016)

CMUDeepLens Architecture
(Lanusse et al. 2017)

Some CMUDeepLens results



True Positive Rate = $\frac{TP}{TP + FN}$

  • $TP$: True Positives
  • $FN$: False Negatives


False Positive Rate = $\frac{FP}{FP + TN}$

  • $FP$: False Positives
  • $TN$: True Negatives

The Euclid strong-lens finding challenge

Metcalf, . . ., Lanusse, et al. (2018)



Better accuracy than human visual inspection !

CMU DeepLens in the wild

Huang et al. (2019) - arXiv:1906.00970

takeaway message



Deep Learning for Low Level Processing
  • An example of Deep Learning allowing us to handle the volume and data rate at the image level

  • Our automated lens finder is faster and more reliable than human volunteers.
    $\Longrightarrow$ Larger and more robust samples for the science analysis.

Hybrid physics-ML models for image inverse problems

Work in collaboration with:
Peter Melchior, Fred Moolekamp




$\Longrightarrow$ Use PixelCNNs as deep priors for deblending

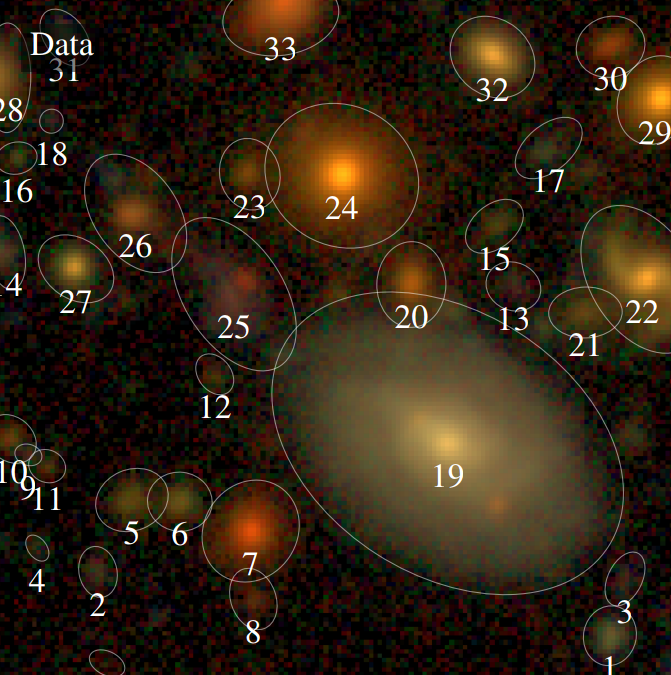
The challenge of galaxy blending

Bosch et al. 2017
  • In HSC over 60% of all galaxies are blended

  • Important impact on our main cosmological probes

  • Current generation of deblenders does not meet our target requirements

    • Existing methods rely on simple assumptions about galaxy profiles, like symmetry or monotonicity
Deblending is an ill-posed inverse problem, akin to Blind Source Separation. The is no single solution.
$\Longrightarrow$ Intuitively, the key will to leverage an understanding of how individual galaxies look like.

Can AI solve all of our problems?

Branched GAN model for deblending (Reiman & Göhre, 2018)
The issue with using deep learning as a black-box
  • No explicit control of noise, PSF, depth, number of sources.
    • Model would have to be retrained for all observing configurations
  • No guarantees on the network output (e.g. flux preservation, artifacts)
  • No proper uncertainty quantification.

Linear inverse problems

$\boxed{y = \mathbf{A}x + n}$

$\mathbf{A}$ is known and encodes our physical understanding of the problem.
$\Longrightarrow$ When non-invertible or ill-conditioned, the inverse problem is ill-posed with no unique solution $x$
Deconvolution
Inpainting
Denoising
$\boxed{y = \mathbf{A}x + n}$

The Bayesian view of the problem:

$$ p(x | y) \propto p(y | x) \ p(x) $$
  • $p(y | x)$ is the data likelihood, which contains the physics

  • $p(x)$ is our prior knowledge on the solution.


With these concepts in hand, we want to estimate the Maximum A Posteriori solution:

$$\hat{x} = \arg\max\limits_x \ \log p(y \ | \ x) + \log p(x)$$
For instance, if $n$ is Gaussian, $\hat{x} = \arg\max\limits_x \ \frac{1}{2} \parallel y - \mathbf{A} x \parallel_{\mathbf{\Sigma}}^2 + \log p(x)$

How do you choose the prior ?

Classical examples of signal priors

Sparse
$$ \log p(x) = \parallel \mathbf{W} x \parallel_1 $$
Gaussian $$ \log p(x) = x^t \mathbf{\Sigma^{-1}} x $$
Total Variation $$ \log p(x) = \parallel \nabla x \parallel_1 $$

But what about this?

Can we use Deep Learning to learn the prior from data?

The evolution of generative models




  • Deep Belief Network
    (Hinton et al. 2006)

  • Variational AutoEncoder
    (Kingma & Welling 2014)

  • Generative Adversarial Network
    (Goodfellow et al. 2014)

  • Wasserstein GAN
    (Arjovsky et al. 2017)



A visual Turing test


Fake PixelCNN samples

Real SDSS

Not all generative models are created equal

Grathwohl et al. 2018


  • GANs and VAEs are very common and successfull but do not fit our purposes.

  • We want a model which can provide an explicit $\log p(x)$.

PixelCNN: Likelihood-based Autoregressive generative model

Models the probability $p(x)$ of an image $x$ as: $$ p_{\theta}(x) = \prod_{i=0}^{n} p_{\theta}(x_i | x_{i-1} \ldots x_0) $$
  • Some of the best log-likelihoods on the market.
  • Extremely stable during training.
  • Slow to sample from.



Ramachandran et al. 2017
van den Oord et al. 2016

  • Provides an explicit value for $\log p_\theta(x)$
    $\Longrightarrow$ Can be used as a Bayesian prior for inverse problems.

A deep denoising example

$$ \boxed{{\color{Orchid} y} = {\color{SkyBlue} x} + n} $$
Try me out at: https://eiffl.github.io/DeepPriors
  • We learn the distribution of noiseless data $\log p_\theta(x)$ from samples using a deep generative model.

  • We measure a noisy ${\color{Orchid} y}$ and we want to estimate a denoised ${\color{SkyBlue} x}$

  • The solution should lie on the realistic data manifold, symbolized by the two-moons distribution.

    We want to solve for the Maximum A Posterior solution:

    $$\arg \max - \frac{1}{2} \parallel {\color{Orchid} y} - {\color{SkyBlue} x} \parallel_2^2 + \log p_\theta({\color{SkyBlue} x})$$ This can be done by gradient descent as long as one has access to $\frac{\color{orange} d \color{orange}\log \color{orange}p\color{orange}(\color{orange}x\color{orange})}{\color{orange} d \color{orange}x}$.

The Scarlet algorithm: deblending as an optimization problem

Melchior et al. 2018
$$ \mathcal{L} = \frac{1}{2} \parallel \mathbf{\Sigma}^{-1/2} (\ Y - P \ast A S \ ) \parallel_2^2 - \sum_{i=1}^K \log p_{\theta}(S_i) + \sum_{i=1}^K g_i(A_i) + \sum_{i=1}^K f_i(S_i)$$
Where for a $K$ component blend:
  • $P$ is the convolution with the instrumental response

  • $A_i$ are channel-wise galaxy SEDs, $S_i$ are the morphology models

  • $\mathbf{\Sigma}$ is the noise covariance

  • $\log p_\theta$ is a PixelCNN prior

  • $f_i$ and $g_i$ are arbitrary additional non-smooth consraints, e.g. positivity, monotonicity...
$\Longrightarrow$ Explicit physical modeling of the observed sky

Training the morphology prior

Postage stamps of isolated COSMOS galaxies used for training, at WFIRST resolution and fixed fiducial PSF
isolated galaxy $\log p_\theta(x) = 3293.7$
artificial blend $\log p_\theta(x) = 3100.5 $

Scarlet in action

Input blend
Solution
Residuals
  • Classic priors (monotonicity, symmetry).

  • Deep Morphology prior.
True Galaxy
Deep Morphology Prior Solution
Monotonicity + Symmetry Solution

Extending to multi-band images

Lanusse, Melchior, Moolekamp (2019)

Takeaway



  • Deep generative models can be used to provide data driven priors.


  • Explicit likelihood, uses of all of our physical knowledge.
    $\Longrightarrow$ The method can be applied for varying PSF, noise, or even different instruments!


  • Iterative optimization can include additional regularization terms.
    • Ensures fit to data (flux preservation).
    • Can impose physical constraints like positivity.




But what about uncertainty quantification?



Can we sample from the full Bayesian posterior $p(y | x)$ to estimate uncertainties?

Deep Posterior Sampling with Denoising Score Matching

Work in collaboration with:
Benjamin Remy, Zaccharie Ramzi




$\Longrightarrow$ Sample from posterior with gradient-based Monte-Carlo methods

The score is all you need!

  • Instead of learning ${\color{orange} \log {\color{orange} p\color{orange}(\color{orange} x\color{orange})}}$, learn $\frac{\color{orange} d \color{orange}\log \color{orange}p\color{orange}(\color{orange}x\color{orange})}{\color{orange} d \color{orange}x}$, a.k.a. the Score Function

    • MAP estimation only need the score! Same is true for Hamiltonian Monte Carlo!

  • The score can be learned efficiently by training a deep Gaussian denoiser (Denoising Score Matching).
  • The score of the full posterior is simply: $$\nabla \log p(x |y) = \underbrace{\nabla \log p(y |x)}_{\mbox{known}} \quad + \quad \underbrace{\nabla \log p(x)}_{\mbox{learned}}$$

$\boldsymbol{x}'$
$\boldsymbol{x}$
$\boldsymbol{x}'- \boldsymbol{r}^\star(\boldsymbol{x}', \sigma)$
$\boldsymbol{r}^\star(\boldsymbol{x}', \sigma)$
$$\boxed{\boldsymbol{r}^\star(\boldsymbol{x}', \sigma) = \boldsymbol{x}' + \sigma^2 \nabla_{\boldsymbol{x}} \log p_{\sigma^2}(\boldsymbol{x}')}$$

Uncertainty quantification in Magnetic Resonance Imaging (MRI)

Ramzi, Remy, Lanusse et al. 2020


$$\boxed{y = \mathbf{M} \mathbf{F} x + n}$$

  • Learn score $\nabla \log p(x)$ with UNet trained by denoising score matching.
  • Sample 320x320pix image posterior by Annealed Hamiltonian Monte Carlo.

$\Longrightarrow$ We can see which parts of the image are well constrained by data, and which regions are uncertain.

Probabilistic Mass-Mapping of the HST COSMOS field

Remy, Lanusse, Ramzi et al. 2020
$$\boxed{\gamma = \mathbf{P} \kappa + n}$$
  • Hybrid prior: theoretical Gaussian on large scale, data-driven on small scales using N-body simulations. $$\underbrace{\nabla_{\boldsymbol{\kappa}} \log p(\boldsymbol{\kappa})}_\text{full prior} = \underbrace{\nabla_{\boldsymbol{\kappa}} \log p_{th}(\boldsymbol{\kappa})}_\text{gaussian prior} + \underbrace{\boldsymbol{r}_\theta(\boldsymbol{\kappa}, \nabla_{\boldsymbol{\kappa}} \log p_{th}(\boldsymbol{\kappa}))}_\text{learned residuals}$$ with $p_{th}(\boldsymbol{\kappa}) = \frac{1}{ \sqrt{ \det 2 \pi \boldsymbol{S}}} \exp \left( -\frac{1}{2} \boldsymbol{\kappa}^\dagger \boldsymbol{S}^{-1} \boldsymbol{\kappa} \right)$, computed from theory.


Conclusion





Where is Deep Learning interesting for Astronomical Image Processing?
  • Extremely efficient at classification tasks.
    $\Longrightarrow$ Improve size and quality of samples for science.

  • Restricting Deep Learning to modeling the priors brings robustness and intrepretability.
    • Deep Generative Models are perfect for learning data-driven priors.

  • Proper Uncertainty Quantification is possible by sampling the Bayesian posterior of the inverse problem.




Thank you!



Bonus: How to train a generative model from noisy/corrupted data?

Deep Generative Models for Galaxy Image Simulations


Open In Colab


Work in collaboration with
Rachel Mandelbaum, Siamak Ravanbakhsh, Chun-Liang Li, Barnabas Poczos, Peter Freeman



Lanusse et al. (2020)
Ravanbakhsh, Lanusse, et al. (2017)

The weak lensing shape measurement problem

Shape measurement biases
$$ < e > = \ (1 + m) \ \gamma \ + \ c $$
  • Can be calibrated on image simulations
  • How complex do the simulations need to be?

Complications specific to astronomical images: spot the differences!


CelebA

HSC PDR-2 wide

  • There is noise
  • We have a Point Spread Function

A Physicist's approach: let's build a model



$\longrightarrow$
$g_\theta$
$\longrightarrow$
PSF
$\longrightarrow$
Pixelation
$\longrightarrow$
Noise
Probabilistic model
$$ x \sim ? $$
$$ x \sim \mathcal{N}(z, \Sigma) \quad z \sim ? $$
latent $z$ is a denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} z, \Sigma) \quad z \sim ?$$
latent $z$ is a super-resolved and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast z), \Sigma) \quad z \sim ? $$
latent $z$ is a deconvolved, super-resolved, and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast g_\theta(z)), \Sigma) \quad z \sim \mathcal{N}(0, \mathbf{I}) $$
latent $z$ is a Gaussian sample
$\theta$ are parameters of the model



$\Longrightarrow$ Decouples the morphology model from the observing conditions.

How to train your dragon model

  • Training the generative amounts to finding $\theta_\star$ that maximizes the marginal likelihood of the model: $$p_\theta(x | \Sigma, \Pi) = \int \mathcal{N}( \Pi \ast g_\theta(z), \Sigma) \ p(z) \ dz$$
    $\Longrightarrow$ This is generally intractable

  • Efficient training of parameter $\theta$ is made possible by Amortized Variational Inference.
Auto-Encoding Variational Bayes (Kingma & Welling, 2014)
  • We introduce a parametric distribution $q_\phi(z | x, \Pi, \Sigma)$ which aims to model the posterior $p_{\theta}(z | x, \Pi, \Sigma)$.

  • Working out the KL divergence between these two distributions leads to: $$\log p_\theta(x | \Sigma, \Pi) \quad \geq \quad - \mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right) \quad + \quad \mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]$$ $\Longrightarrow$ This is the Evidence Lower-Bound, which is differentiable with respect to $\theta$ and $\phi$.

The famous Variational Auto-Encoder



$$\log p_\theta(x| \Sigma, \Pi ) \geq - \underbrace{\mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right)}_{\mbox{code regularization}} + \underbrace{\mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]}_{\mbox{reconstruction error}} $$

Sampling from the model

Woups... what's going on?

Tradeoff between code regularization and image quality


$$\log p_\theta(x| \Sigma, \Pi ) \geq - \underbrace{\mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right)}_{\mbox{code regularization}} + \underbrace{\mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]}_{\mbox{reconstruction error}} $$

Latent space modeling with Normalizing Flows


$\Longrightarrow$ All we need to do is sample from the aggregate posterior of the data instead of sampling from the prior.


Dinh et al. 2016
Normalizing Flows
  • Assumes a bijective mapping between data space $x$ and latent space $z$ with prior $p(z)$: $$ z = f_{\theta} ( x ) \qquad \mbox{and} \qquad x = f^{-1}_{\theta}(z)$$
  • Admits an explicit marginal likelihood: $$ \log p_\theta(x) = \log p(z) + \log \left| \frac{\partial f_\theta}{\partial x} \right|(x) $$




Flow-VAE samples



Second order moments


Testing galaxy morphologies





Bayesian Inference a.k.a. Uncertainty Quantification

The Bayesian view of the problem: $$ p(z | x ) \propto p_\theta(x | z, \Sigma, \mathbf{\Pi}) p(z)$$ where:
  • $p( z | x )$ is the posterior
  • $p( x | z )$ is the data likelihood, contains the physics
  • $p( z )$ is the prior
Data
$x_n$
Truth
$x_0$

Posterior samples
$g_\theta(z)$

$\mathbf{P} (\Pi \ast g_\theta(z))$
Median
Data residuals
$x_n - \mathbf{P} (\Pi \ast g_\theta(z))$
Standard Deviation
$\Longrightarrow$ Uncertainties are fully captured by the posterior.

How to perform efficient posterior inference?

(Böhm, Lanusse, Seljak 2019)
  • Posterior fitting by Variational Inference
    $$ \mathrm{ELBO} = - \mathbb{D}_{KL}\left( q_\phi(z) \parallel p(z) \right) \quad + \quad \mathbb{E}_{z \sim q_{\phi}} \left[ \log p_\theta(x_n | z, \Sigma_n, \Pi_n) \right]$$
  • Posterior fitting by $EL_{2}O$
    $$EL_2O = \arg \min_\theta \mathbb{E}_{z \sim p^{\prime}} \sum_i \alpha_i \parallel \nabla_{z}^n \ln q_\theta(z) - \nabla_{z}^{n} \ln p(z | x_n, \Sigma_n, \Pi_n) \parallel_2^2$$See (Seljak & Yu, 2019) for more details.

  • Or your favorite method...